Ongoing work with Team at Rice:
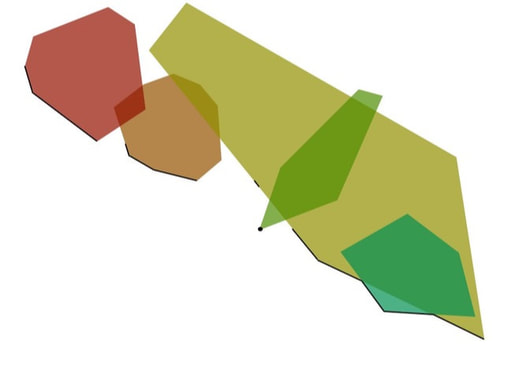
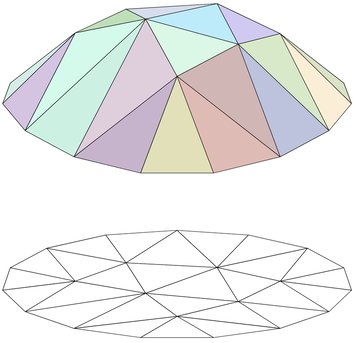
Machine Learning for Network Optimization. Minimum spanning tree (MST) has been studied for decades, but sensitivity analyses for changes to the edge costs have been mostly local. I am studying the use of a neural network (NN) to provide a global sensitivity analysis for MST and other weighted matroid optimization problems. From the functional properties of linear programming value functions (right), we impose constraints on the architecture and training of convex NNs. We furthermore use a tailored loss function to improve training outcomes. 
Algorithm Design for Multiobjective Optimization. Weight space decomposition algorithms provide an intuitive and objective method for making sense of a nondominated frontier, especially for triobjective integer programs. Previous work established the weight space decomposition for supported points in the nondominated frontier (by using the weighted sum scalarization), but this leaves out many points and gives a distorted view of their value in the weight space. This motivated my work with using weighted Tchebychev scalarization for a new weight space decomposition. This results in a much more complex geometry, where convexity is lost but we found many convexity-like properties. Using this approach, we provide a dual perspective to many existing findings in the primal perspective of solving for the nondominated frontier of a triobjective integer programs. 

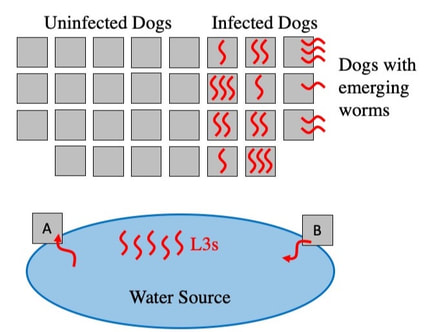
Epidemiological Simulation Modeling. Guinea worm is a parasite that infects humans and many mammals via transmission through water sources. Thanks to The Carter Center's Guinea Worm Eradication Program, the countries with active infections have been reduced to just a few countries in Africa. Chad, specifically, was challenged by infections entering the dog population, where infection monitoring and control is much more difficult. We developed an agent-based simulation model to represent the life cycle of Guinea Worm and trained the multi-water source model to accurately fit regional infection data. More recent work asks which interventions should be prioritized in different regions, where equity is measured.

​This work has been published in The American Journal of Tropical Medicine and Hygiene. 
Algorithm Design for Multiobjective Optimization. Biobjective mixed integer programming began receiving great attention beginning in 2015. Like all multiobjective optimization approaches, the goal is to find the nondominated frontier, a.k.a., the Pareto optimal frontier. Unlike purely discrete problems, however, mixed integer problems have a nondominated frontier with continuous portions. I introduced the Boxed Line Method, which remains a major competitor in this class of algorithms. Furthermore, the recursive variant of the Boxed Line Method has a linear bound on the number of IPs solved with respect to the number of line segments in the nondominated frontier. This was  the first complexity result of its kind for this class of algorithms. 

This work was published in the INFORMS Journal on Computing, and received the INFORMS Computing Society Student Paper Award.
PhD work:
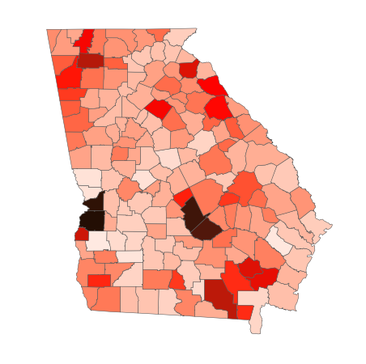
Public Health Data Analysis. The COVID-19 pandemic has been challenging for experts and the general public, alike. One challenge has been the deluge of infection data made available, which complicates the daily task of making sense of this data and making sound conclusions from it. To this end, I developed an interactive COVID-19 dashboard specifically for the counties of Georgia. This tool includes basic data from the Georgia Department of Public Health, but also goes further by using published ranking and prediction methods. The dashboard makes all levels of the data clear to explore, as well as the ranked risk for each of the 159 counties, and some future projections, as well. 

What else inspires me?

I write about social good applications of mathematical optimization on my medium blog.
Posts are written at an introductory level, designed for the non-expert. 
The narratives lay the groundwork for ways in which mathematical modeling and linear programming
​can be used to solve real-world problems.